We say that a distribution is symmetric, if it is equally balanced on both sides of the mean. This means that the frequency of observations on both sides is equal.

However, if the frequency of occurrence of observations is more in a particular direction then the distribution is asymmetric. This asymmetry of the distribution on either side of the mean is called skewness.

A symmetric distribution has no tail on either side. Such a distribution is not skewed in any direction. This is the same as a normal distribution i.e. a distribution which has zero skewness.

Suppose we are looking at a distribution of returns with a mean return of 0. If there is a large frequency of occurrence of negative returns compared to positive returns then the distribution displays a fat left tail or negative skewness.

In case the frequency of positive returns exceeds that of negative returns then the distribution displays a fat right tail or positive skewness.

Skewed Distribution

Skewness is a measure of degree of asymmetry of a distribution. It measures the degree to which a distribution leans towards the left or the right side.

While skewness is a measure of asymmetry, kurtosis is a measure of the ‘peakedness’ of the distribution.

Both skewness and kurtosis are measured relative to a normal distribution. Just like a distribution can be negatively or positively skewed, it can be Leptokurtic or Platykurtic depending on whether the peakedness is more than or less than the normal distribution.

Leptokurtic: The distribution is more peaked than a normal distribution.

Platykurtic: The distribution is less peaked than a normal distribution.

For a normal distribution, the computed kurtosis is 3. So, its excess kurtosis is 0. So, a Leptokurtic distribution will have excess kurtosis greater than 0 and a Platykurtic distribution will have excess kurtosis less than 0.

Calculating Sample Skewness and Kurtosis

The formulae for calculating skewness and kurtosis are given below:

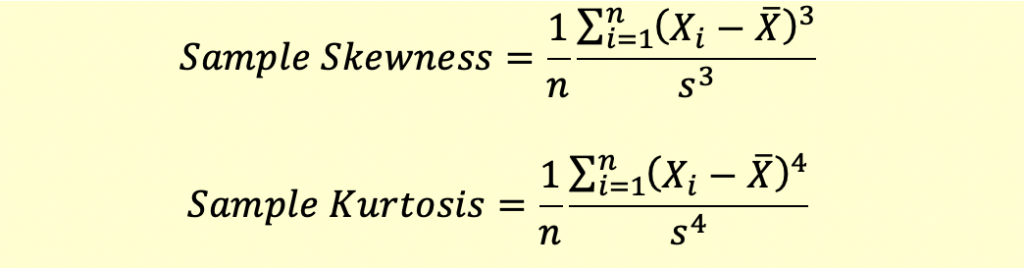
Some Observations

• Sample skewness can be positive or negative. Positive skewness means that the distribution is right skewed.
• A skewness of 0.5 or more indicates significant skewness.
• For a normal distribution kurtosis is 3. We calculate excess kurtosis as Sample Kurtosus – 3. A positive excess kurtosis indicates that the distribution is Leptokurtic and a negative excess kurtosis indicates that the distribution is Platykurtic.
• An excess kurtosis of 1 or more is considered high.