Chebyshev’s Inequality
Chebyshev’s Inequality is used to describe the percentage of values in a distribution within an interval centered at the mean.
It states that for a distribution, the percentage of observations that lie within k standard deviations is atleast 1 – 1/k2
This is illustrated below:
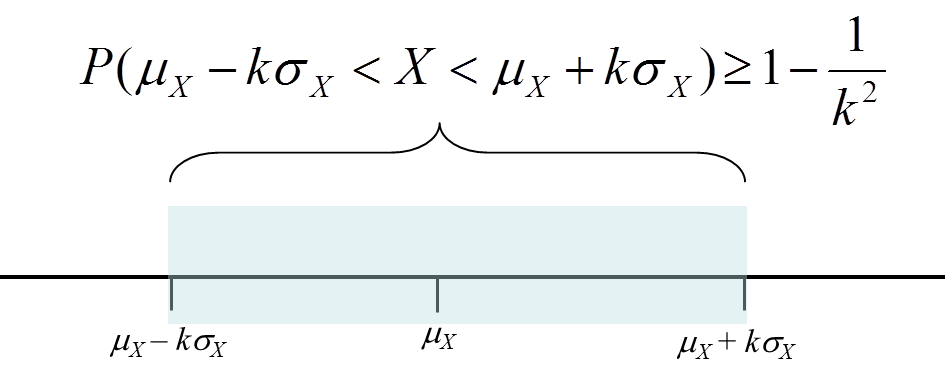
Example
The following table shows the minimum number of observations that lie within a certain number of standard deviations of the mean.
| Standard Deviations | % of observations |
| 1.5 | 56% |
| 2 | 75% |
| 3 | 89% |
| 4 | 94% |
An important feature of Chebyshev’s Inequality is that it works with any kind of distribution.
LESSONS
- Descriptive Vs. Inferential Statistics
- Types of Measurement Scales
- Parameter, Sample Statistic, and Frequency Distribution
- Relative Frequencies and Cumulative Relative Frequencies
- Properties of a Data Set (Histogram / Frequency Polygon)
- Measures of Central Tendency
- Calculating Arithmetic Mean
- Calculating Weighted Average Mean
- Calculating Geometric Mean
- Calculating Harmonic Mean
- Calculating Median and Mode of a Data Set
- Quartiles, Quintiles, Deciles, and Percentiles
- Range and Mean Absolute Deviation
- Variance and Standard Deviation
- Chebyshev’s Inequality
- Coefficient of Variation
- Sharpe Ratio
- Skewness and Kurtosis
- Relative Locations of Mean, Median and Mode
R Programming Bundle: 25% OFF
Get our R Programming - Data Science for Finance Bundle for just $29 $39.
Get it now for just $29