Coefficient of Variation

We earlier learned about calculating the variance and standard deviation for a set of data. Standard deviation as a measure of dispersion is much easier to interpret as it uses the same unit of measurement as the data itself. However, standard deviation is not a good measure if we are comparing the relative degree of variation of two sets of data or distributions. For this purpose we have another measure called the coefficient of variation. The coefficient of variation measures the degree of variation in a distribution relative to the mean of the distribution.

Suppose we have two data sets A and B. The coefficient of variation for these data sets is calculated as follows:

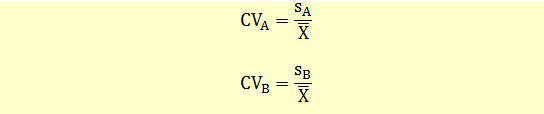
The coefficient of variations of two distributions can be compared to find out which one has less dispersion per unit of risk.

Let’s say standard deviation of A is 2% with a mean of 6% and standard deviation of B is 1.5% with a mean of 4%.

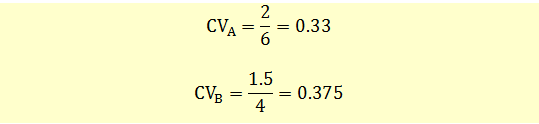
We can see that distribution A has less dispersion per unit of return than distribution B.