Calculating Arithmetic Mean
Arithmetic mean is the simple average of all observations and is calculated by adding all the observations and dividing it by the total number of observations.
We can calculate arithmetic mean for both the population and the sample.
Population Mean
This is the arithmetic mean of all observations in the population. The formula for population mean is given below:
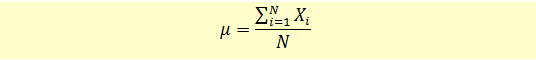
Sample Mean
This is the arithmetic mean of all observations in the sample of the population. The formula for sample mean is given below:
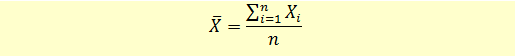
Notice the difference in notations between the two formulas:
Xi represents the observations in both formulas.
The number of observations in the population is represented by capital N, while the number of observations in the sample is represented by small n.
Example
Population Dataset: 1.5, 2.5, 3, 2.3, 4.3, 5.6, 4.2, 6.7, 5.9, 1.2, 5.4, 9.8, 8.5, 5.5, 2.9, 1.7, 8.8, 6.2, 9.5, 3.8
We can draw a sample from the above data set.
Sample Dataset: 2.5, 5.6, 1.2, 9.8, 8.8
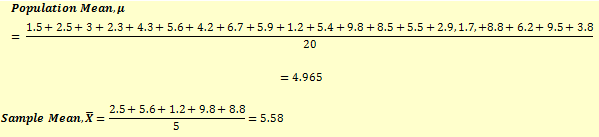
Some observations:
- As you can see, there is a lot of difference in population mean and sample mean. This can happen for small data sets or if the sample is not drawn correctly.
- Arithmetic mean is very sensitive to extreme values as a very large or small value can significantly pull the mean on either side.
- For arithmetic mean, the sum of deviations from the mean is always zero, i.e.,
- Arithmetic mean is preferred over median and mode, as it uses all information about the observations such as size and magnitude.
- There can be only one arithmetic mean for a data set.


