This lesson is free - just sign in to access it.
This lesson is a part of the course Statistical Concepts and Market Returns
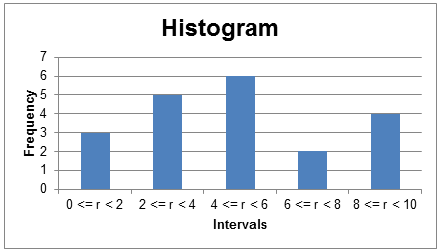
The data in a frequency distribution can be presented using a histogram. A histogram is a bar chart with different intervals on the X-axis and the absolute frequencies on the Y-axis. The histogram for our data is presented below:
A frequency polygon is similar to a histogram, except that the x-axis plots the mid-point for each interval. Instead of bars, the neighbouring points are connected by lines.
