Quartiles, Quintiles, Deciles, and Percentiles
A quantile refers to a value at or below which a stated fraction of the data lies. Quantile is a general term, and we have different types of quantiles referring to different fractions.
| Quartiles | Divides the distribution into quarters. |
| Quintiles | Divides the distribution into fifths. |
| Deciles | Divides the distribution into tenths. |
| Percentiles | Divides the distribution into hundredths. |
Percentiles are the most commonly used quantiles and other quantiles are also expressed in terms of percentiles.
For example, the first quartile is the value at or below which a quarter or 25 percent of the values in the distribution lie. The second quartile will have 50 percent of values below it (50 percentile).
Example 1
Suppose we have a data set with 20 observations and we want to calculate third quartile or 75 percentile. Since the total number of observations (20) is divisible by 4, the calculation is simple. The 15th value is the third quartile because 3/4th of the values lie at or below the 15th value.
Example 2
The calculation of a quartile may however be difficult, if the total number of observations is not divisible by 4. For large data sets, this will not matter. However, for a small data set the quartile value will only be an approximation.
Let’s say our data set has 15 observations and we want to calculate the third quartile.
1.2, 1.5, 1.7, 2.3, 2.5, 2.9, 3, 3.8, 4.2, 4.3, 5.4, 5.5, 5.6, 5.9, 6.2
Since 15 is not divisible by 4, we cannot directly observe the third quartile. We will use a slightly different method to calculate this.
We know that third quartile is 75 percentile.
We can calculate the position of an observation at a given percentile using the following formula.
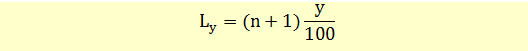
Where y is the percentile we want to find and n is the number of observations in a dataset. In our data set, n = 15, and y = 75.
Ly = (15+1)*(75/100) = 12
The 12th observation is 5.5. That means 75 percent of observations lie below 5.5.
In this example Ly was a whole number. If it was not, we would have used linear interpolation to find the quartile.


