Multivariate Linear Regression in Python with scikit-learn Library
In this post, we will provide an example of machine learning regression algorithm using the multivariate linear regression in Python from scikit-learn library in Python. The example contains the following steps:
Step 1: Import libraries and load the data into the environment.
Step 2: Generate the features of the model that are related with some measure of volatility, price and volume.
Step 3: Visualize the correlation between the features and target variable with scatterplots.
Step 4: Create the train and test dataset and fit the model using the linear regression algorithm.
Step 5: Make predictions, obtain the performance of the model, and plot the results.
Step 1: Import libraries and load the data into the environment.
We will first import the required libraries in our Python environment.
1import pandas as pd
2from datetime import datetime
3import numpy as np
4from sklearn.linear_model import LinearRegression
5import matplotlib.pyplot as plt
6We will work with SPY data between dates 2010-01-04 to 2015-12-07.
First we use the read_csv() method to load the csv file into the environment. Make sure to update the file path to your directory structure.
1SPY_data = pd.read_csv("C:/Users/FT/Documents/MachineLearningCourse/SPY_regression.csv")
2
3# Change the Date column from object to datetime object
4SPY_data["Date"] = pd.to_datetime(SPY_data["Date"])
5
6# Preview the data
7SPY_data.head(10)
8The data has the following structure:
1 Date Open High Low Close Volume Adj Close
20 2015-12-07 2090.419922 2090.419922 2066.780029 2077.070068 4.043820e+09 2077.070068
31 2015-12-04 2051.239990 2093.840088 2051.239990 2091.689941 4.214910e+09 2091.689941
42 2015-12-03 2080.709961 2085.000000 2042.349976 2049.620117 4.306490e+09 2049.620117
53 2015-12-02 2101.709961 2104.270020 2077.110107 2079.510010 3.950640e+09 2079.510010
64 2015-12-01 2082.929932 2103.370117 2082.929932 2102.629883 3.712120e+09 2102.629883
75 2015-11-30 2090.949951 2093.810059 2080.409912 2080.409912 4.245030e+09 2080.409912
86 2015-11-27 2088.820068 2093.290039 2084.129883 2090.110107 1.466840e+09 2090.110107
97 2015-11-25 2089.300049 2093.000000 2086.300049 2088.870117 2.852940e+09 2088.870117
108 2015-11-24 2084.419922 2094.120117 2070.290039 2089.139893 3.884930e+09 2089.139893
119 2015-11-23 2089.409912 2095.610107 2081.389893 2086.590088 3.587980e+09 2086.590088
12Let's now set the Date as index and reverse the order of the dataframe in order to have oldest values at top.
1# Set Date as index
2SPY_data.set_index('Date',inplace=True)
3
4# Reverse the order of the dataframe in order to have oldest values at top
5SPY_data.sort_values('Date',ascending=True)
6Step 2: Generate features of the model
We will generate the following features of the model:
- High - Low percent change
- 5 periods Exponential Moving Average
- Standard deviation of the price over the past 5 days
- Daily volume percent change
- Average volume for the past 5 days
- Volume over close price ratio
1SPY_data['High-Low_pct'] = (SPY_data['High'] - SPY_data['Low']).pct_change()
2SPY_data['ewm_5'] = SPY_data["Close"].ewm(span=5).mean().shift(periods=1)
3SPY_data['price_std_5'] = SPY_data["Close"].rolling(center=False,window= 30).std().shift(periods=1)
4
5SPY_data['volume Change'] = SPY_data['Volume'].pct_change()
6SPY_data['volume_avg_5'] = SPY_data["Volume"].rolling(center=False,window=5).mean().shift(periods=1)
7SPY_data['volume Close'] = SPY_data["Volume"].rolling(center=False,window=5).std().shift(periods=1)
8Step 3: Visualize the correlation between the features and target variable
Before training the dataset, we will make some plots to observe the correlations between the features and the target variable.
1jet= plt.get_cmap('jet')
2colors = iter(jet(np.linspace(0,1,10)))
3
4def correlation(df,variables, n_rows, n_cols):
5 fig = plt.figure(figsize=(8,6))
6 #fig = plt.figure(figsize=(14,9))
7 for i, var in enumerate(variables):
8 ax = fig.add_subplot(n_rows,n_cols,i+1)
9 asset = df.loc[:,var]
10 ax.scatter(df["Adj Close"], asset, c = next(colors))
11 ax.set_xlabel("Adj Close")
12 ax.set_ylabel("{}".format(var))
13 ax.set_title(var +" vs price")
14 fig.tight_layout()
15 plt.show()
16
17# Take the name of the last 6 columns of the SPY_data which are the model features
18variables = SPY_data.columns[-6:]
19
20correlation(SPY_data,variables,3,3)
21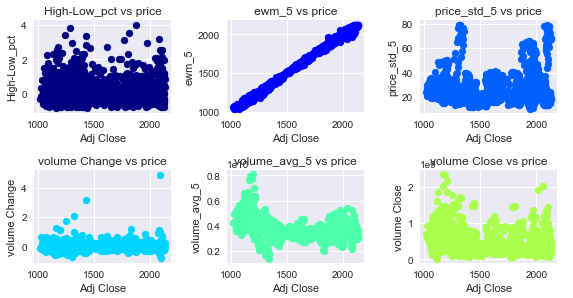
Correlations between Features and Target Variable (Adj Close)
The correlation matrix between the features and the target variable has the following values:
1SPY_data.corr()['Adj Close'].loc[variables]
2
3High-Low_pct -0.010328
4ewm_5 0.998513
5price_std_5 0.100524
6volume Change -0.005446
7volume_avg_5 -0.485734
8volume Close -0.241898
9Either the scatterplot or the correlation matrix reflects that the Exponential Moving Average for 5 periods is very highly correlated with the Adj Close variable. Secondly is possible to observe a negative correlation between Adj Close and the volume average for 5 days and with the volume to Close ratio.
Step 4: Train the Dataset and Fit the model
Due to the feature calculation, the SPY_data contains some NaN values that correspond to the first’s rows of the exponential and moving average columns. We will see how many Nan values there are in each column and then remove these rows.
1SPY_data.isnull().sum().loc[variables]
2
3High-Low_pct 1
4ewm_5 1
5price_std_5 30
6volume Change 1
7volume_avg_5 5
8volume Close 5
9
10# To train the model is necessary to drop any missing value in the dataset.
11
12SPY_data = SPY_data.dropna(axis=0)
13
14# Generate the train and test sets
15
16train = SPY_data[SPY_data.index < datetime(year=2015, month=1, day=1)]
17
18test = SPY_data[SPY_data.index >= datetime(year=2015, month=1, day=1)]
19dates = test.index
20Step 5: Make predictions, obtain the performance of the model, and plot the results
In this step, we will fit the model with the LinearRegression classifier. We are trying to predict the Adj Close value of the Standard and Poor’s index. # So the target of the model is the "Adj Close" Column.
1lr = LinearRegression()
2
3X_train = train[["High-Low_pct","ewm_5","price_std_5","volume_avg_5","volume Change","volume Close"]]
4
5Y_train = train["Adj Close"]
6
7lr.fit(X_train,Y_train)
8
9Create the test features dataset (X_test) which will be used to make the predictions.
1# Create the test features dataset (X_test) which will be used to make the predictions.
2
3X_test = test[["High-Low_pct","ewm_5","price_std_5","volume_avg_5","volume Change","volume Close"]].values
4
5# The labels of the model
6
7Y_test = test["Adj Close"].values
8Predict the Adj Close values using the X_test dataframe and Compute the Mean Squared Error between the predictions and the real observations.
1close_predictions = lr.predict(X_test)
2
3mae = sum(abs(close_predictions - test["Adj Close"].values)) / test.shape[0]
4
5print(mae)
6
718.0904
8We have that the Mean Absolute Error of the model is 18.0904. This metric is more intuitive than others such as the Mean Squared Error, in terms of how close the predictions were to the real price.
Finally we will plot the error term for the last 25 days of the test dataset. This allows observing how long is the error term in each of the days, and asses the performance of the model by date.
1# Create a dataframe that output the Date, the Actual and the predicted values
2df = pd.DataFrame({'Date':dates,'Actual': Y_test, 'Predicted': close_predictions})
3df1 = df.tail(25)
4
5# set the date with string format for plotting
6df1['Date'] = df1['Date'].dt.strftime('%Y-%m-%d')
7
8df1.set_index('Date',inplace=True)
9
10error = df1['Actual'] - df1['Predicted']
11
12# Plot the error term between the actual and predicted values for the last 25 days
13
14error.plot(kind='bar',figsize=(8,6))
15plt.grid(which='major', linestyle='-', linewidth='0.5', color='green')
16plt.grid(which='minor', linestyle=':', linewidth='0.5', color='black')
17plt.xticks(rotation=45)
18plt.show()
19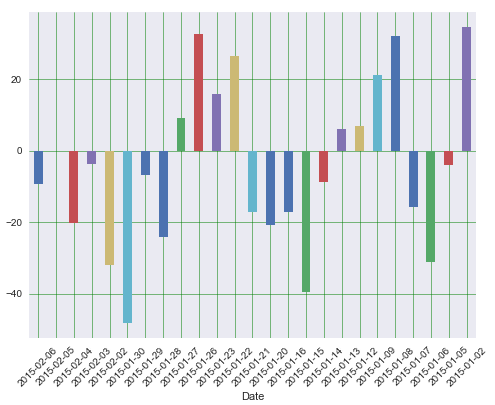
Error Term by date
This concludes our example of Multivariate Linear Regression in Python.
Unlock Premium Content
Upgrade your account to access the full article, downloads, and exercises.
You'll get access to:
- Access complete tutorials and examples
- Download source code and resources
- Follow along with practical exercises
- Get in-depth explanations