Standard Error of the Sample Mean

The standard error of the sample mean is calculated using the following formula.

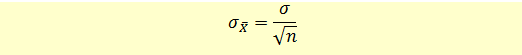
Note that the larger the sample size, the smaller will be the standard deviation.

Let’s say the monthly average savings of a family in a city are $500. Based on a sample size of 50 families, the standard error will be:

Standard Error = 500/(Sqrt(50) = $70.71

This means that if we take all possible samples of size 50 each, calculate the sample means of each sample and create a sampling distribution, then this sampling distribution will have a mean of $500 and a standard error of $70.71.

In reality, since we don’t have the population standard deviation, we use the standard deviation of the sample mean to calculate the standard error.