Confidence Interval for a Population mean, with an Unknown Population Variance

If the population variance is not known, then we do the following change to the above confidence interval formula:

1. Substitute the population variance (s) with the sample variance (s)
2. Us t-distribution instead of normal distribution (explained in the following pages)

We use t-distribution because the use of sample variance introduces extra uncertainty as s varies from sample to sample.

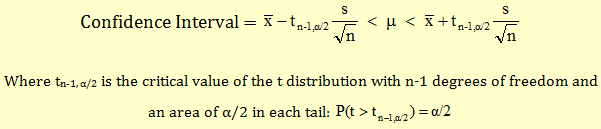
Example

We take a sample of 16 stocks from a large population with a mean return of 5.2% and a standard deviation of 1.2%. The population standard deviation is not known.

Calculate the 95% confidence interval for the population mean.

The confidence interval will be:

The value of t is observed from the t-table.