Confidence Interval Estimates
Along with point estimate we may also want to find a range of values within which our population parameter lies with a certain confidence level (1 – α). This is called confidence interval estimate. The α is known as the significance level and the probability (1-α) is known as the degree of confidence or confidence level. An interval estimate provides more information about a population characteristic than does a point estimate.
For example, we can say that the population mean is between 8 and 10 with a 95% confidence. 95% is the degree of confidence and 5% is the level of significance.
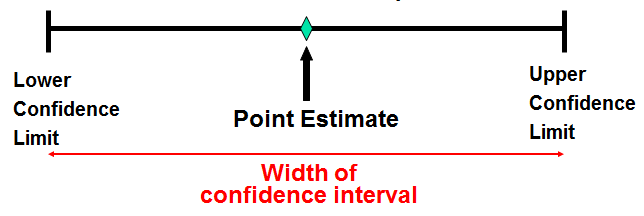
Confidence intervals are derived from point estimates using the following general formula:

We will learn about how to calculate the confidence interval for a population mean, given a normal distribution, under three situations:
- Population variance is known
- Population variance is not known
- Population variance is not known and sample size is large


