Multiplication, Addition and Total Probability Rules

This lesson is free - just sign in to access it.

This lesson is a part of the course Probability Concepts

Want full access? Our premium membership gives you unlimited access to all courses, quizzes, and downloadable resources.

The additional rule determines the probability of atleast one of the events occuring.

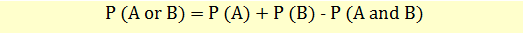
If A and B are mutually exclusive, then P(A and B) = 0, so the rule can be simplified as follows:

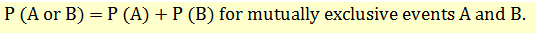
Multiplication rule determines the joint probability of two events.