Calculating Covariance and Correlation
Both correlation and covariance are indicators of the relationship between two variables. They indicate whether the variables are positively or negatively related, i.e., how they move together. For example, what is the relationship between the performance of gold and S&P 500 index?
Covariance measures the comovement between two variables i.e. the amount by which the two random variables show movement or change together.
The correlation also indicates the degree to which the two variables are related. It’s a translation of covariance into a unit-less measure that we can understand (-1.0 to 1.0). The correlation of the variable with itself is always 1.
Calculating Covariance and Correlation
Covariance is calculated using the following formula:

Where Ri and Rj represent the returns on two assets, i and j.
The following example illustrates the calculation of expected returns:
| State of Economy | RA | RB | RA-E(RA ) | RB-E(RB ) | P*( RA-E(RA ))( RB-E(RB )) | |
| 1 | 10% | -10% | 5% | -26.00% | -9.00% | 0.234% |
| 2 | 30% | 15% | 12% | -1.00% | -2.00% | 0.006% |
| 3 | 30% | 18% | 19% | 2.00% | 5.00% | 0.030% |
| 4 | 20% | 22% | 15% | 6.00% | 1.00% | 0.012% |
| 5 | 10% | 27% | 12% | 11.00% | -2.00% | -0.022% |
| E(RA) =16% | E(RB)=14% | Cov = 0.0026 |
Once we have the covariance, we can calculate the correlation as follows:
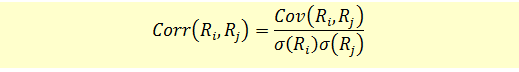
We already have the covariance. The standard deviations of the two returns can be calculated using the formulas learned under section ‘Variance and Standard Deviation’.
Std (Ri) = 9.40%
Std (Rj) = 4.17%
Correlation = 0.0026/(9.4%*4.17%) = 0.66
Refer to the Covariance Correlation spread sheet for detailed calculations.
Covariance Interpreted
In financial markets covariance is positive when the variables show similar behaviour i.e. larger values of one variable correspond to larger values of another variable and the same holds true for smaller values. When the covariance is negative it means the exact opposite i.e. larger values of one variable correspond to smaller values of another variable.
The strength of the linear relationship however cannot be easily interpreted by the magnitude of the calculated value. In order to interpret the strength a related measure called correlation is used.
Correlation Interpreted
The correlation number would always be in the range of -1 to +1. A value of 1 means that the variables always move in the same direction and a value of -1 means the two always move in the opposite direction. In the case where the variables are independent the covariance is zero which means the correlation is also zero. In other words the two variables do not exhibit any movement relative to each other. Any number in between indicates that the one number moves less positively or negatively in relation to changes in another number.


