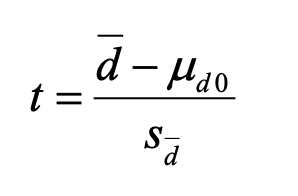- What is Hypothesis Testing
- Test Statistic, Type I and type II Errors, and Significance Level
- Decision Rule in Hypothesis Testing
- p-Value in Hypothesis Testing
- Selecting the Appropriate Test Statistic
- Hypothesis Testing with t-statistic
- Hypothesis Testing with z-statistic
- Tests Concerning Differences in Means
- Paired Comparision Tests - Mean Differences When Populations are Not Independent
- Hypothesis Tests Concerning Variances
- Chi-square Test – Test for value of a single population variance
- F-test - Test for the Differences Between Two Population Variances
- Non-parametric Tests
Paired Comparision Tests - Mean Differences When Populations are Not Independent
In the above cases, we assumed that the samples are independent. However, sometimes the samples may not be independent.
If the samples are not independent, a test of mean difference is done using paired observations. Such a test is called paired comparison test.
- H0: µd = µd0 versus HA: µd ≠ µd0
- H0: µd ≤ µd0 versus HA: µd > µd0
- H0: µd ≥ µd0 versus HA: µd < µd0
In the first hypothesis we want to test if the mean of the differences in pairs is zero.
µd is the mean of the population of paired differences.
µd0 is the hypothesized value of mean of paired differences. This is usually assumed to be zero.
Calculating t-statistic
To calculate the t-statistic, we first need to find the sample mean difference:
The sample variance is:
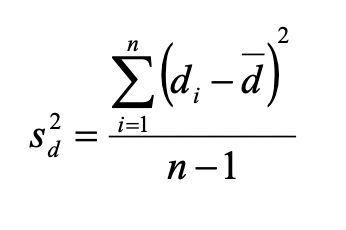
The standard deviation of the mean is:
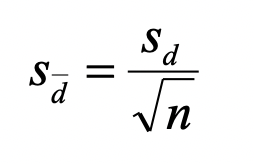
The test statistic, with n – 1 df is:
Related Downloads
Related Quizzes
Free Guides - Getting Started with R and Python
Enter your name and email address below and we will email you the guides for R programming and Python.