- What is Hypothesis Testing
- Test Statistic, Type I and type II Errors, and Significance Level
- Decision Rule in Hypothesis Testing
- p-Value in Hypothesis Testing
- Selecting the Appropriate Test Statistic
- Hypothesis Testing with t-statistic
- Hypothesis Testing with z-statistic
- Tests Concerning Differences in Means
- Paired Comparision Tests - Mean Differences When Populations are Not Independent
- Hypothesis Tests Concerning Variances
- Chi-square Test – Test for value of a single population variance
- F-test - Test for the Differences Between Two Population Variances
- Non-parametric Tests
F-test - Test for the Differences Between Two Population Variances
The tests concerning the differences between two population variances are called F-test. We are testing the equality of two variances.
For this test, we calculate a F-distributed test statistic that follows the F-distribution.
Here also we assume that the samples are normally distributed and are independent.
The hypothesis is formed as follows:
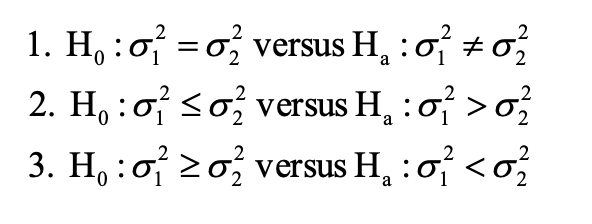
Assume we have two samples with n1 and n2 observations. The test statistic for F-test is calculated as follows:
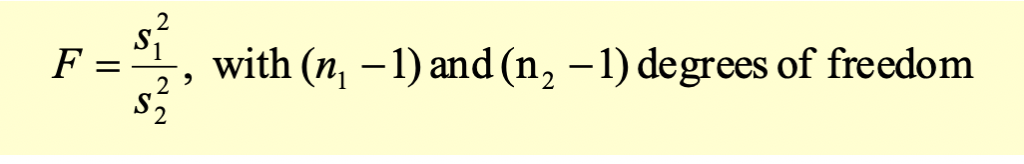
We use the degrees of freedom to identify the critical value from the F-table.
The F distribution is an asymmetric distribution that has a minimum value of 0, but no maximum value. The curve reaches a peak not far to the right of 0, and then gradually approaches the horizontal axis the larger the F value is. The F distribution approaches, but never quite touches the horizontal axis.
All the other steps in conducting the hypothesis test are the same, except the calculation of test statistic.
Related Downloads
Related Quizzes
Free Guides - Getting Started with R and Python
Enter your name and email address below and we will email you the guides for R programming and Python.