Standard Normal Distribution

A normal distribution can be described using just two parameters, namely (μ), mean and variance (σ2).

In a normal distribution, these two variables could take any value. For example, for a normally distributed stock portfolio, the mean could be 10% and the standard deviation could be 20%.

A standard normal distribution is a standardized form of normal distribution with a mean μ = 0 and standard deviation σ = 1.

We can standardize any normal random variable, by computing a z-score for it. z-scores make it easier to compare data values measured on different scales. A z-score reflects how many standard deviations above or below the mean a raw score is. The z-score is positive if the data value lies above the mean and negative if the data value lies below the mean. Z-score is represented using the following formula:

Where x represents the observation, m is the population mean, and s is the standard deviation.

Suppose the dividends paid by a company every year are normally distributed with a mean of $10 and a standard deviation of $2. If the company pays a dividend of $14 this year, what will be its z-score?

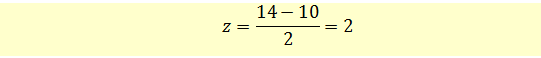
A z-score of 2 indicates that the current dividends are 2 standard deviations above the mean.