Option Greeks: Gamma
An option’s delta changes as the stock price changes. Gamma is a measure of the rate of change in the delta with respect to changes in the underlying price.
Gamma is the second derivative of the option premium with respect to the stock price. It is the first derivative of delta with respect to the stock price.
Gamma is represented as follows:
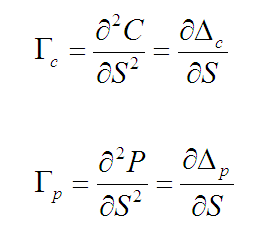
Gamma is also called curvature. It is an important measure because it corrects the convexity of the option value.
Gamma is a measure of how often option portfolios need to be adjusted as stock prices change and time passes.
While establishing an effective delta-hedge for a portfolio, a trader may also want to neutralize the portfolio's gamma. This will ensure that the hedge will be effective over a wider range of underlying price movements.
Gamma will be larger for the at-the-money options, and gets lower as the options move in- and out-of-the-money options. Unlike delta, gamma is always positive for both calls and puts.
Options with gammas near zero have deltas that are not particularly sensitive to changes in the stock price
For a given striking price and expiration, the call gamma equals the put gamma.
Calculating Gamma
For calls and puts, gamma is calculated using the following formula:
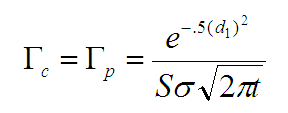
Downloads
Resources
Options Pricing and Geeks Spreadsheet
Download the options pricing and geeks spreadsheet.


