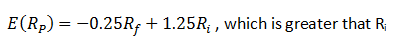Capital Allocation Line with Two Assets
We know that an investor can combine many risky assets to create a portfolio with lower risks. By varying the weights of different assets in the portfolio many portfolios with different risk-return profiles can be created. If we plot the risk-return profiles of these different portfolios, what we get is an efficient frontier. The efficient frontier represents the set of portfolios that will give the highest return at each level of risk or the lowest risk for each level of return.
Let’s assume that investor chooses to invest in a risky portfolio that lies on this efficient frontier. Let’s call it Ri.
The investor can combine the risky portfolio, Ri, with a risk-free asset Rf, to create a new portfolio, RP.
The risk-return profile of this combined portfolio of risk assets and risk-free asset will be as follows:

In the above equation, the risk (standard deviation) for the risk-free asset is 0. So, the equation will be reduced to the following:

We can create different portfolios with different weights for the risk-free asset and the risky portfolio. The following graph shows the risk-return of the portfolio by varying the weight from 0 to 100%. The line is called the Capital Allocation Line.

Any portfolio can be created on this line by varying the proportion of funds invested in risk-free asset and risky asset.
The Capital Allocation Line (CAL) can be explained using the standard regression equation Y = MX + C, as follows:
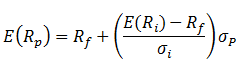
Note that when you invest in a risk-free asset, you are actually lending money to the government. For this reason, any portfolio created between Rf and Ri is called a lending portfolio. An investor can earn returns higher than the risky portfolio by borrowing money at the risk-free rate and investing this money in the portfolio of risky assets. This is represented in the following chart: