Nominal Interest Rate and Effective Yield

When you go to a bank enquiring about the deposit rates, the rates specified by the bank can be expressed in two ways: nominal interest rate, and the effective annual yield.

The difference between the two is that the nominal rate does not take the compounding into consideration, while the effective annual yields take the effect of compounding into consideration.

Consider an investment of $100 at a nominal rate of 10% compounded monthly.

The future value of the investment will be:

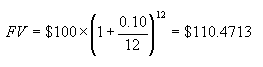
The effective yield will be the absolute increase as a percentage of the principal invested.

Therefore, the effective annual yield will be:

EY = 10.4713/100 or 10.4713%

Since the effective yield considers compounding effect, it will always be greater than nominal yield.

The effective yield can be calculated using the following formula:

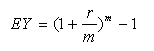
Why Calculate Effective Annual Yield?

Effective yield is useful when you are considering various investment options where the interest rates are expressed at different compounding rates. In such a situation, you can convert all the rates into effective annual yields and then make an informed decision.

Form example, assume that you have a choice between investing in a bond A offering a nominal interest rate of 5% compounded semiannually, and another bond B offering a nominal interest rate of 4.9% compounded monthly. Since the compounding periods are different, a direct comparison is difficult. Therefore, will calculate the effective annual yields for both the bonds:

EY (Bond A) = (1+0.05/2)^2 – 1 = 5.0625%

EY (Bond B) = (1+0.049/12)^12 – 1 = 5.0848%

We can see that the effective yield for Bond B is higher, so, that’s a better investment.

The nominal interest is also know as Annual Percentage Rate (APR). The Effective Annual Yield is also known as Annual Percentage Yield (APY).