Independent and Identically Distributed Variables

Definition

I.I.D’s or independent and identically distributed variables are commonly used in probability theory and statistics and typically refer to the sequence of random variables. If the sequence of random variables has similar probability distributions but they are independent of each other then the variables are called independent and identically distributed variables.

This is a pre-reqeusitie for many key theorems like the Central Limit theorem which form the basis of concepts like the normal distribution and many other statistical theories. It must be noted that this assumption does not always hold true in the real world i.e. in practice. This is however the default model for random variables.

Characteristics

Sum of I.I.D’s

The sum of independent and identically distributed functions has a moment generating function and it has a continuous probability density function.

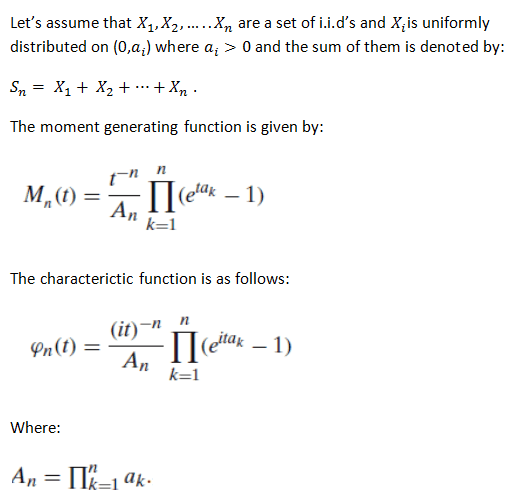
It can be shown that the characteristic function is absolutely integrable and the i.i.d follows a continuous and bounded uniform continuous density function given by:

Expected Value and Variance of average of I.I.D’s

As above let’s assume that there are n independent and identically distributed random variables and we take the average of them.

The resulting variable is given by the following equation:

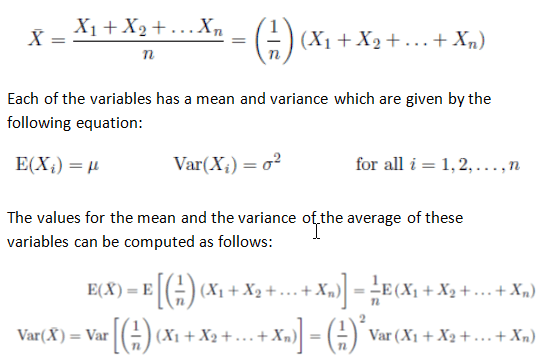
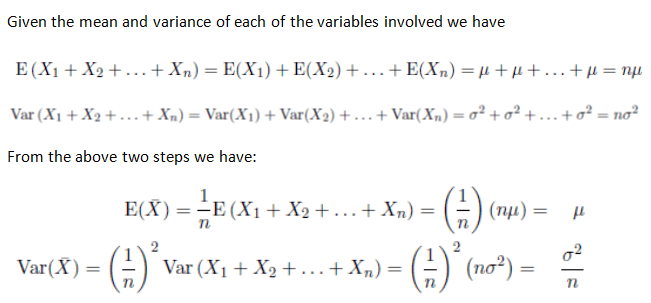
Financial Volatility

Financial series data are adequately expressed by Gaussian distributions. In order to calculate the volatility of a series of financial data like the Brazilian real / US$ exchange rates they are expressed as a series of reduced independent and identically distributed variables which form a best fit for the real world data.

Exponential law when applied to this set of reduced variables helps explain their volatilities. It is to be noted that this is based on the assumption that the stochastic process always exhibits a characteristic period.

Applications

Some of the most common uses of I.I.D’s are illustrated in their use in the following situations:

• A series of consequent fair or unfair tosses of a coin
• A series of consequent fair or unfair rolls of dice
• A series of results of fair or unfair roulette wheel spins

Some of the other most common applications are in signal or image processing and in testing the hyotheses of the means of random variables which assumes the central limit theorem.