Using Beta Distribution for Estimating Recovery Rates
Most of the people use the beta distribution to model recovery rates.
In probability theory and statistics, the beta distribution is a family of continuous probability distributions defined on the interval (0, 1) parameterized by two positive shape parameters, typically denoted by α and β.
The function for the beta distribution is as follows:
c is the normalization constant.
We can input different values of α and β to obtain different shapes of recovery rates.
The mean and standard deviation of the dataset can be used as the two parameters α and β of the beta distribution using the BETADIST() function in excel. The following graph shows four shapes of the curves based on the different values of mean and standard deviation.
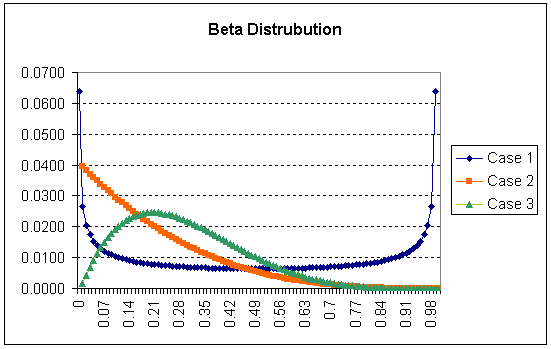
This method is considered quite flexible because it only requires the mean and variance for calibration.
Beta Distribution Spreadsheet
Download the following spreadsheet to see how the distribution is arrived at. This spreadsheet shows the estimation of recovery rates using beta distribution.
Lesson Resources
Data Science in Finance: 9-Book Bundle
Master R and Python for financial data science with our comprehensive bundle of 9 ebooks.
What's Included:
- Getting Started with R
- R Programming for Data Science
- Data Visualization with R
- Financial Time Series Analysis with R
- Quantitative Trading Strategies with R
- Derivatives with R
- Credit Risk Modelling With R
- Python for Data Science
- Machine Learning in Finance using Python
Each book includes PDFs, explanations, instructions, data files, and R code for all examples.
Get the Bundle for $39 (Regular $57)Free Guides - Getting Started with R and Python
Enter your name and email address below and we will email you the guides for R programming and Python.
