The Minimum Variance Frontier & Efficient Frontier

Two asset classes (stocks and bonds for example) can be combined with varying proportions to create an infinite number of portfolios.

An investor can calculate the expected returns and variances of a two asset portfolio and plotting these on the Y (returns) and X (variances) axis of a graph.

Global Minimum Variance Portfolio: The portfolio with the lowest risk/variance on the efficient frontier.

Efficient Frontier: Starting with the global minimum variance portfolio and extending to the portfolio of 100% stocks, the efficient frontier is the series of optimal portfolios that can be constructed from two assets, each offering the highest returns for a given amount of risk.

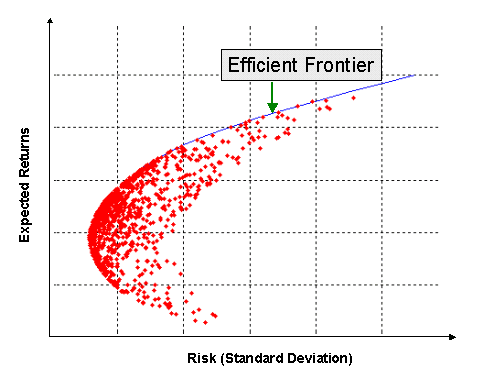
Note that in a two asset case, a portfolio of 100% bonds will fall on the minimum variance frontier, but be excluded from the efficient frontier as applying some small portion of stocks to the portfolio will offer higher returns and a lower level of risk through the benefits of diversification.

Multi Asset Portfolios (three or more asset classes)

• In a two asset class portfolio, all of the portfolio combinations will lie on the minimum variance frontier.
• For three or more asset classes, many portfolio combinations will be inefficient and fall inside the frontier.
• For a three asset class portfolio, the highest and lowest possible returning portfolios will lie on the minimum variance frontier.

No portfolios can be above the efficient frontier.

As an investment rule, only portfolios on the efficient frontier should be considered.

Instability of the Minimum Variance Frontier and Portfolio Implications

When calculating portfolios on the minimum variance frontier, it must be recognized that the output values are highly sensitive to the data input values for returns, variances, and correlations.  Small changes to these values can create large shifts in the frontier.

Data Input Challenges

• Sampling techniques to obtain return, variance, and correlation data can fall victim to sampling error.
• The values of these inputs change over time.

The optimal portfolio often requires taking short positions, which is not practical or not allowable for many portfolio managers.

Regularly changing estimates to inputs can indicate a need to rebalance frequently, which is expensive.