An outlier is an observation in a dataset that lies abnormally away from other observations in the dataset. Based on this definition, it is the analyst who decides what constitutes an outlier in the data that he is working with. The analyst observes the data and outlines the characteristics of what is considered normal for an observation. As an example, if your dataset contains heights of men in a city, you may observe that most men have a height in the range of 5 feet to 6 feet. You may keep some margin and say that anyone who is above 6.5 feet is considered an outlier.

While analyzing data, it is sometimes important to remove these outliers as they tend to skew the statistics you’re calculating. In this article, we will learn about how to identify and remove outliers in R programming.

How to Identify Outliers in R

There are two ways we can identify outliers. One is using Interquartile Range (IQR) and the other is using z-scores.

Let’s look at these two methods:

Interquartile Range

Interquartile range (IQR) is the difference between the 1st quartile (25th percentile) and the 3rd quartile (75th percentile). It basically gives us the spread of the middle 50% values in the dataset. For a value to be identified as an outlier the rule of thumb is that the value is outside 1.5 times IQR above the 3rd quartile or 1.5 times IQR below the 1st quartile.

Outlier = Value above Q2 + 1.5IQR Or Value below 1.5IQR

Z-score

We can also identify outliers using z-scores. A z-score reflects how many standard deviations above or below the mean an observation is. A z-score of 2 indicates that the current observation is 2 standard deviations above the mean.

The rule of thumb is that an observation is an outlier if it has a z-score less than -3 or greater than 3.

How to Remove Outliers in R

Now that we know how to identify outliers, let’s learn about how we can remove these outliers from a dataset in R.

For our example, let’s create dataframe that contains some random data.

# set seed to 0 so that we can reproduce the results of this example

set.seed(0)

# create a data frame with one column containing 1000 observations

data <- data.frame(X=rnorm(1000, mean=20, sd=3)

The rnorm function generates a vector of normally distributed random numbers. In this example it will generate 1000 values with a mean of 20 and a standard deviation of 3.

You can check the first few values of the dataframe using the head command.

head(data)

  X
1 23.78886
2 19.02130
3 23.98940
4 23.81729
5 21.24392
6 15.38015

This will give you an idea of the kind of values we have in the dataset.

Now let’s use the two methods to remove the outliers from this dataset.

Remove Outliers using Interquartile Range Method

To identify the outlier, we will first calculate Q1, Q2, the IQR and then compare each value to check if it is above Q3-1.5IQR or if it is below Q1-1.5IQR.

We have formulas for calculating quartiles and IQR in R.

#Calculate Q, Q3 and IQR

Q1 <- quantile(data$X, .25)

Q3 <- quantile(data$X, .75)

IQR <- IQR(data$X)

Now that we have these statistics, we can apply our rules and create a new dataframe that doesn’t contain any values that are outside our desired range.

#Remove rows that have values outside of 1.5*IQR of Q1 and Q3

new_data <- subset(data, data$X> (Q1 - 1.5*IQR) & data$X< (Q3 + 1.5*IQR))

You can use the dimensions function on this new dataset to see how many values it has left.

dim(new_data)

[1] 994  1

As you can see, it has 994 observations left, which means that the remaining 6 observations were identified as outliers and removed.

Remove Outliers using Z-score Method

We calculate z-score using the following formula:

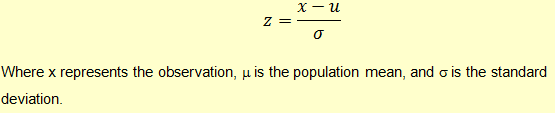
To identify and remove outliers using the z-score, we will need to calculate the z-score of each value in our dataset, and then remove values that are above 3 or below -3.

In R, we can calculate the absolute values of z-scores for each observation and then remove the rows that have absolute z-score > 3.

# set seed to 0

set.seed(0)

# create a data frame with random values

data <- data.frame(X=rnorm(1000, mean=20, sd=3))

# Preview the data

head(data)

# add a new column to the data frame containing the z-score

data$zscore <- (abs(data$X-mean(data$X))/sd(data$X))

# Check the data again. It should now have two columns: X and zscore

head(data)

X  zscore

1 23.78886 1.2813403
2 19.02130 0.3110243
3 23.98940 1.3483190
4 23.81729 1.2908343
5 21.24392 0.4313316
6 15.38015 1.5271674

# create a new dataframe that contains only those rows 
# that have a z-score of below 3

new_data <- subset(data, data$zscore < 3)

# check the new dataset

dim(new_data)

[1] 997  2

As you can see, 3 outliers have been removed from the data.

There are various reasons why outliers can come into your data. It could be due to human error, or genuine abnormalities, for example, extreme spikes in stock market data. You should be careful about these outliers and remove them if you think that they can impact your analysis.