This is a brief recap of Modern Portfolio Theory (MPT) before delving into practical applications of it. While there are many aspects of MPT, the focus will be on its application for portfolio optimisation. The origin of MPT came from a paper written by Harry Markowitz in 1952 to create an optimal portfolio. From thereon, he continued to expand on this theory until, eventually, it became known as MPT and occur in the aspects that are now common knowledge.

The first aspect relating to MPT is that, by increasing one’s number of assets in a portfolio, one can reduce the risk of the overall portfolio. This is because assets are, generally speaking, not perfectly correlated. As such, through diversification, one can remove the level of stock-specific risk. Mathematically, this is represented by the variance equation of a portfolio:

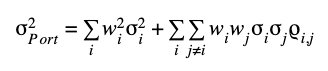
Where σ is the standard deviation of the asset, w is the weight of the asset and ρ is the correlation between 2 assets. As long as ρ is not equal to 1, the addition of a new asset will reduce the portfolio risk until it equals only the market risk.

The expected return of the portfolio is calculated as follows:

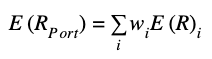
We can now plot the expected return and expected variance of a whole combination of portfolios. Below is an example of this:

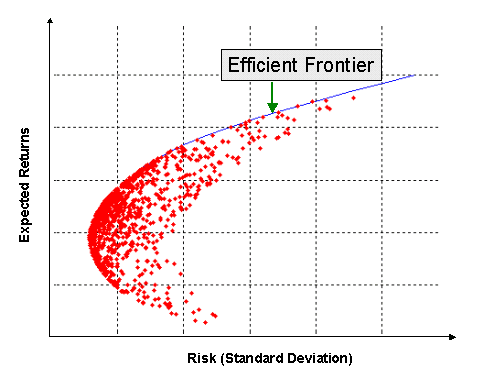
The individual dots represent potential combinations of assets that make up a hypothetical portfolio. The better portfolio is always considered the one to the top-right, as it has less risk and a greater expected return. The portfolios that are considered best for each level of risk (i.e. highest expected return per unit of risk) form the solid line known as the efficient frontier. These are the optimal portfolios that an investor can choose from. The specific choice of the portfolio depends on the return profile and risk appetite of the investor.

From this relationship, there are two generally used portfolio optimisations. These are minimum-variance and mean-variance optimisation. In minimum variance, the portfolio that is selected is the one that has the lowest risk. For a highly risk-averse investor, this would be an optimal portfolio. In mean-variance optimisation, the optimal portfolio is the portfolio with the highest ratio between expected return and risk. It is often termed as the greatest risk-adjusted portfolio.