Breakeven Analysis

For a firm, the breakeven point is the quantity of the sales required by the firm to cover its total cost, i.e., Total revenue = Total cost. At this quantity of sales the firm's net income is zero.

We know that:

$Q(P-VC) - F = EBIT$

F includes both fixed operating cost and fixed financing cost.

Breakeven quantity is the quantity where EBIT = 0. So, we solve for Q where EBIT = 0.

$Q=\frac{(\text{Total Fixed Cost})}{(P-VC)}$

Example

Let's say we have the following data about a company:

Price per unit = $8

Variable costs = $6

Fixed operating costs = $20,000

Fixed financing costs = $60,000

The breakeven quantity will be calculated as follows:

$Q = \frac{80,000}{8-6} = \text{40,000 Units}$

The following graph summarizes the relationship between sales, costs, net income and net losses.

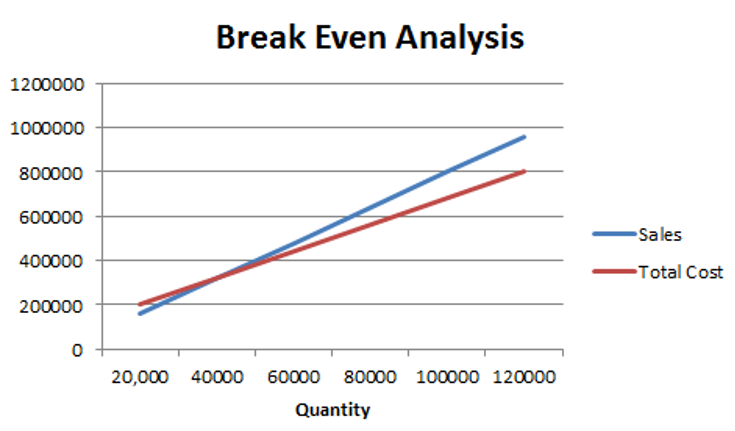
We can make the following observations from the above graph:

• A firm with higher operating and financial leverage will have higher breakeven quantity.

• Leverage magnifies the impact of change in sales on change in net income.

We can also modify the above formula to calculate the operating breakeven quantity:

$Q=\frac{(\text{Fixed Operating Cost})}{(P-VC)}$

In the above example, the operating breakeven quantity will be:

$Q = \frac{20,000}{(8 - 6)} = \text{10,000 units}$