Taylor Series Expansion

In financial markets participants would like to measure the effect of changes in the price of the bond due to changes in yield. This enables better risk management of financial assets as the impact of asset values is determinable.

Recomputing the value of the bond using the changed yield comes across as an obvious solution. However, in practice a method called the Taylor series expansion can be used for this purpose. This expansion represents a non-linear relationship between the yield and price of a bond around its initial value.

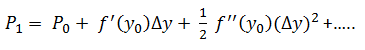
The English mathematician Brook Taylor published this result in 1715 and the full realization of this came only in year 1755 when Euler applied it to differential calculus.

The other way of stating what the Taylor expansion actually implies is to assume that the price function can be written in polynomial form, i.e.

Where the coefficients are unknown when Δy is set to 0 the result gives α0.  If the derivative of both sides is taken and Δy is set to 0 then we derive α1, the first derivative with respect to y0 and the next step gives 2α2 = f''(y0).  In this context, the derivative refers to the mathematical expression and has nothing to do with the financial product derivative.

The first derivative measures the duration and the second derivative measures the convexity and there are situations where there are more than one variable in this equation.

The term f'(.) is the first derivative of price with respect to the yield and the term f"(.) refers to second derivative of the price with respect to the yield of the function f(.)  which has an initial value.

The Taylor expansion is an infinite expansion with increasing powers of Δy of which only the first two terms are used by industry practitioners as they are good indicators of asset price changes relative to other assumptions made for valuing financial assets. The convexity term is negligible for very small changes in price.

The Taylor expansion is one of the fundamental methods used in risk management and is used in different ways in financial markets. It is also used to approximate the movement in value of a derivatives contract, i.e., an option on a stock. The equation then becomes:

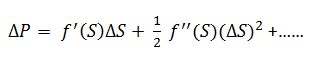
Where S is price of the underlying asset and the first derivative is called the delta and the second derivative is called the gamma.

The expansion is also useful in a situation where a number of financial instruments are involved. If there are N different bonds and there are a certain units of each bond and then the first derivative would be the sum of the units of each bond multiplied by the first derivative of the value of the bond.