Sensitivity Measures for Fixed Income Investments

The derivatives associated with fixed income instruments have special terminology for them. The negative of the first derivative is called the Dollar Duration (DD).

 Where  is called the modified duration. Thus dollar duration is:

 The price is the dirty price of the bond including any accrued interest. The dollar value of the basis point measures the risk associated with the instrument for a basis point change in yield. One basis point is referred to as one hundredth of a percent and the measure can be scaled up across portfolios.

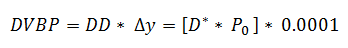
The change in duration to the change in yield, in other words the second derivative of price to yield, is a measure of convexity and the formula for dollar convexity is as follows:

 Whenever the price-yield function is known the first and second order derivatives can be computed. The conventional definition of duration is the average time to receipt of the cash flows.

For a zero coupon bond maturing at time T the duration is the same as time to maturity T whereas the modified duration is the conventional duration divided by  (1+y) and is also called Macaulay duration.

The modified duration is derived as follows:

Modified duration is the appropriate measure of interest rate exposure. When the interest rate is quoted annually the duration is in years and with semi-annual compounding it is for half year periods. The duration with semi-annual compounding has to be divided by 2 to convert it into years.  The relation of modified duration to Macaulay duration can be expressed using the following equation:

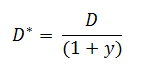
The quantity (1+y) appears in the denominator because the derivative of the present value term was taken with discrete compounding.

If continuous compounding is used the two measures yield the same value. In practice the difference between Macaulay and modified duration is very small.

For a zero-coupon bond the second derivative with respect to the yield is called convexity and is measured in periods squared. For semi-annual compounding convexity is in semesters squared and a division by 4 converts it into years squared. Convexity should be positive for bonds with fixed coupons.

The Taylor expansion for the change in price of the bond is obtained by putting all these terms together and is as follows:

It is very clear from the above equation that the first order linear effect is duration and the second order effect is represented by convexity.