While building a model in data science, our goal is to fit the model to our data in such a way that the model learns the general pattern/trend in the data. However, this doesn't always happen. In some cases, the model will very closely follow the training data to the nose rather than just learning the trends. Suppose you fit the model to a training set. Then, in this case, the model will fit well on the training data, i.e., when evaluated on the training data, it will produce accurate results. However, when you use the model to predict your target variable in test data set, the model will perform poorly. This is called overfitting, i.e, the model is overfitted to the training data. Another way to look at is that the model remembers way too much about the data and fails to learn any meaningful pattern in it.

To prevent overfitting, we make use of techniques generally known as regularization. Regularization involves adding some noise to the objective function of the model before optimizing it. In other words, we are adding a penalty on the different parameters of the model. By adding this penalty, and thereby reducing the freedom of the model, we are able to reduce fitting of the noise to the training data and make it more general.

For a model, the goal of a model developer is to minimize its loss function:

min(Loss(Data|Model))

With regularization, we want to minimize Loss + Complexity (Penalty term)

min(Loss(Data|Model) + complexity(model))

There are three regularization parts:

1. L1 Regularization, also known as Lasso
2. L2 Regularization, also know as Ridge
3. The L1/L2 Regularization, also known as Elastic Net

L1 Regularization

A regression model that uses L1 Regularization is called L1 or Lasso Regression.The L1 regularization adds a penalty equal to the sum of the absolute value of the coefficients. This helps us in selecting features of a model as it shrinks the less important features and completely removing some features (making them zero). In mathematical terms, Lasso Regression adds “absolute value” of coefficient as penalty term to the loss function.

Lambda is the regularization parameter that you provide as an input to the model. Increase in lambda results in reduced overfitting. Lambda is also called regularization rate. We multiply the regularization term (In this case L1) by lambda ( scalar) that tunes the overall impact of regularization. Increasing the lambda value strengthens the regularization effect and vice verse.

L2 Regularization

A regression model that uses L12 Regularization is called L2 or Ridge Regression. The L2 regularization forces the parameters to be relatively small. The bigger the penalization, the smaller the coefficients are. In mathematical terms, Ridge regularization adds a penalty equal to the sum of the squared value of the coefficients to the loss function.

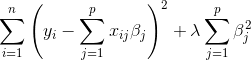
It is important to choose the value of Lambda. If Lambda is very large, it will add too much weight and lead to under-fitting. The L2 regularization technique works well to avoid the over-fitting problem.

Elastic Net Regularization

Elastic Net is a mix of both L1 and L2 regularization. In this case, we apply a penalty to the sum of the absolute values and to the sum of the squared values.

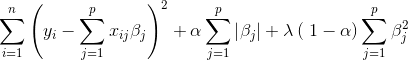
Lambda is the shared penalization parameter. Alpha is used to set the ratio between L1 and L2 regularization.

Let's say we have a linear model with coefficients β1 = 0.1, β2 = 0.4, β3 = 4, β4 = 1 and β5 = 0.8.

The L2 regularization term will be:

\= 0.1^2 + 0.4^2 + 4^2 + 1^2 + 0.8^2

\= 0.01 + 0.16 + 16 + 1 + 0.64

\= 17.81

The third coefficient, 4, with a squared value of 16 adds most of the complexity.