The payoff profile of the options can be used to create more complex positions. A long position in the underlying asset can be decomposed into a long call plus a short put with the same strike price and maturities.

Pay on purchase of a call option is as follows:

Pay on sale of put option is as follows:

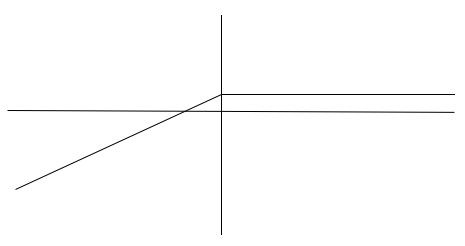
Assume that the strike price and maturities of both the options are the same, below is the payoff profile of combining both these options which is essentially the payoff of going long on the asset.

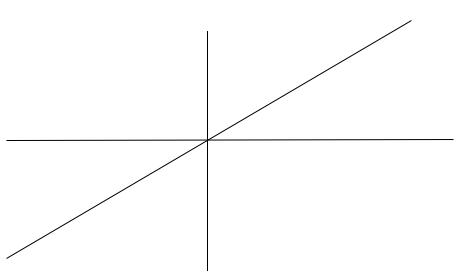
The long call provides the equivalent of the upside and the short put generates the downside risk of holding the asset. This is known as put-call parity.

Consider a portfolio of a long position in the call, a short position in the put and an investment that will ensure that they will be able to pay the exercise at maturity. The initial payoff of this position is as follows:

1. Pay-off on the purchase of the call: -c
2. Pay-off on the sale of the put: +p
3. Payoff on the investment that will pay the strike at the maturity:  (-K present values to today)

The total payoff of this strategy is as follows:

(-c + p + (- K present values to today at the prevailing interest rate)

This payoff is equal to the payoff of going long on an asset = (-S)

There are two possible cases: the call is exercised or the put in exercised. In both the cases the final payoff is that of holding a long position in the asset.

Scenario 1: The Spot on the maturity date is less than the Strike.

In this situation the call is not exercised and the put is exercised. The final payoff is as follows:

Payoff of the call (0) + Payoff the put (- (K-Spot Rate At Maturity)) + Payoff from the investment (K)

The total payoff is the payoff of the Asset - S

Scenario 2: The Spot on the maturity date is greater than the Strike

In this situation the call is exercised and the put is not exercised. The final payoff is as follows:

Payoff of the call (Spot Rate at maturity - K) + Payoff the put ( 0) + Payoff from the investment (K)

The total payoff is the payoff of the Asset: S

With the Put-Call parity equation it is possible to find the value of a call given the put and the value of a put given the value of a call. This relationship holds only for European options and not for American options as American options can be exercised anytime between trade and maturity date.

This relationship can be used to determine the implied dividend yield from the market prices (the interest rate). This can also be used to determine the forward rate in dividend swaps, which are contracts where the payoff is indexed to the actual dividends paid over the horizon, minus the implied dividends.