Economic Interpretation of Sensitivity Measures

Duration can be interpreted as the average time receipt of each cash flow weighted by its present value.  This applied to all cash flows is called Macaulay duration.

The duration of a coupon paying bond can be written as:

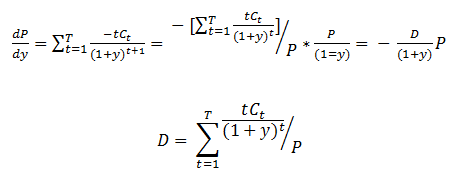
This equation can also be re-written as follows:

Each weight is the present value of each cash flow with respect to the total.

In case of bonds that pay a fixed coupon rate the duration is always less than maturity. If there is a zero coupon bond having a certain maturity then the duration is equal to that tenor of the bond. In case of a coupon paying bond with the same maturity the coupons add weight to prior cash flows so it reduces the duration value. There is also an inverse relationship between yields and duration i.e. for the same bond with lower yields duration is higher than when the yields are higher.  For bonds that have longer maturity the relationship is more visible. This also has an effect on modified duration.

For consols even though there is no yield to maturity the duration is finite and this serves as a cap on the duration of a long-term bond with the same yield. Below is the derivation for the duration of the consol.

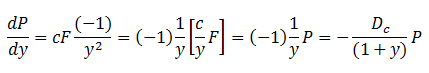
The Macaulay duration is given by:

The relationship linking the sensitivity measures and coupons and yields is as follows – Assuming all others characteristics of the fixed-income instrument are the same duration and convexity are directly proportional to maturity and have an inverse relationship with coupons and yields.

For example, given the same maturity a zero-coupon bond will always have a higher duration then a coupon paying bond and for bonds with higher coupons the duration tends to be lower.

Convexity is positively related to time to maturity. The longer the maturity the larger the payoffs and therefore the convexity are greater and the curvature effect is always beneficial because as per this effect convexity will always be positive. In the case of instruments with uncertain cash flows like mortgage backed securities or bonds that can be called convexity assumes negative values.  So if a zero coupon bond and a 6 percent bond with the same maturities are compared then the zero coupon bond will always have a higher convexity because there is only one cash flow at maturity and it will roughly be equal to the square of maturity.