Bayes Theorem – Calculating Conditional Probabilities
The Situation
The field of science attempts to answer the following question which arises very often. Given a set of data and observations regarding them the law surrounding the type of data needs to be deduced. In other words the model the fits the data description needs to be derived.
Broadly speaking there are two different approaches to this type of problem. The first one is when a model is assumed from the behavior determined from the observations and the probability of getting the data out of the model is calculated. The other approach aims to find the probability of the model given the data. The first approach is called the Fequentist approach and the second one is called the Bayesian method.
The two methods are contrasted by their characteritics which are listed below:
Frequensitst method
- A model is assumed but the parameters of the model which are fixed may be unknown.
- Data errors that might be random in nature are possible but they have a certain probability distribution for example Gaussian.
- Fitting the model to the data is done by the mathematical methods.
Bayesian Method
- The model is never assumed and there are no true parameters as well. All parameters are however treated as random variables with probability distributions
- Since the model parameters themselves are random with their own distribution, the random errors in data have no probability distribution
- Fitting the data to the model is done by the mathematical methods.
- Both methods give the same answer in the real world but it may be argued that the Bayesian method is more applicable to answering such real-life questions.
The Theorem
Bayes theorem can be represented by the following equation:
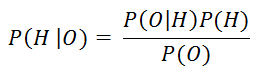
Where:
- H is the Hypothesis and O is the observation.
- P (H|O) is the Posterior Probability of H, i.e., the probability of a hypothesis (H) given an observation (O). This represents your updated degree of belief.
- P(O|H) is the likelihood of H, i.e., the probability of an observation given a hypothesis. In other words, the probability that the hypothesis confers upon the observation.
- P (H) is the prior probability of H, i.e., the probability of a hypothesis (H) before the observation. (Not necessarily an a priory concept, can sometimes be based on previous empirical evidence).
- P(O) is the unconditional probability of O, i.e., the probability of the observation irrespective of any particular hypothesis.
This theorem states that the probability of the hypothesis given an observation is equal to the division of the product of the probabaility of the observation given the hypothesis and the probability of the hypothesis divided by the probability of the observation itself.
A more general form the theorem is as shown below:
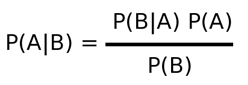
- The probability of A given that B has happened is equal to the division of the product of the probability of B given A has happened and the probability of A by the probability of B alone.
- A and B can be observations, events or any other forms of data we observe in the real world.
- The probablity of one real world variable given another one is called a conditional probability.
Worked Example
The following information is available regarding drug testing.
- 0.5% of people are drug users
- A test has 99% accuracy. 99% of drug users and 99% of non-drug users are correctly identified by it.
The problem question is to find the probability of being a drug user if you’ve tested positive?
The solution according to Baye’s theorem is as follows:
- p(pos|user)=0.99 (99% effective at detecting users)
- p(user)=0.005 the probability of a number of people being drug users
- p(pos)=0.01*0.995+0.99*0.005 = 0.0149 which is deduced from the following details: 1% chance of non-users, 99.5% of the population, to be tested positive, plus 99% chance of the users, 0.5% of the population, to be tested positive.
- P(user/pos) = 0.99*0.005/0.0149 = 0.33
The answer we arrive at is that there is only a 33% chance that a positive test is correct
In this example some information is available about the proportions of users versus non-users but in practice such information may not be available or determined.


