Minimum Variance Hedge Ratio

One problem with using futures contracts to hedge a portfolio of spot assets, is that a perfect futures contracts may not exist, that is, a perfect hedge cannot be achieved. For example, if an airline wishes to hedge its exposure to variation in jet fuel prices, it will find that there is no jet fuel futures market. A variation on the theme might go as follow. Although there exists a futures market for an underlying asset, that futures market is so illiquid that it is functionally useless.

Thus, we need to find way to use sub-optimal contracts, contracts that are highly correlated with the underlying asset and who have a similar variance. This is achieved using the minimum variance hedge ratio.

The minimum variance hedge ratio (or optimal hedge ratio) is the ratio of futures position relative to the spot position that minimizes the variance of the position.

The minimum variance hedge ratio is given as follows:

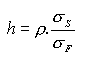
Where, $\rho$ is the correlation and $\sigma$ is the standard deviation

Let us take an example to understand this.

An airlines company wishes to hedge their annual 2,000,000 gallons jet fuel requirement. In short they fear that the price of jet fuel will rise.

Unfortunately, there exists no jet fuel futures contract.

However, a futures contract for heating oil trades at the NYMEX (New York Mercantile Exchange) and, it is known that jet fuel is a derivative of heating oil..

The contract size of the NYMEX heating oil contract is 42,000 gallons. Thus, if heating oil were a perfect hedge, the Airline would purchase 2,000,000/42,000 contracts = 47.61 contract (either 46 or 47 contracts)

Since heating oil is not a perfect hedge, they would use the minimum-variance hedge ratio to calculate the optimal number of contracts to purchase. i.e.,

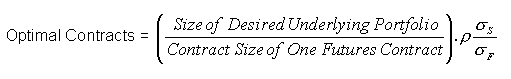
The airlines company collects 15 month’s worth of data on spot jet fuel (S) and heating oil futures (F) prices.

Month	Δ in Future Price (ΔF)	Δ in Spot Jet Fuel Price (ΔS)
1	0.021	0.029
2	0.035	0.020
3	-0.046	-0.044
4	0.001	0.008
5	0.044	0.026
6	- 0029	-0.019
7	-0.026	-0.010
8	-0.029	-0.007
9	0.048	0.043
10	-0.006	0.011
11	-0.036	-0.036
12	-0.011	-0.018
13	0.019	0.009
14	-0.027	-0.032
15	0.029	0.023

We calculate the following:

σF = 0.0313

σS = 0.0263

ρ = 0.928

So the Optimal number of contract is: = 37.14

Rounding, Airlines company would buy: 37 heating oil futures contracts

If indeed jet fuel prices rose over the course of the year. The losses Airline would incur due to the higher spot jet fuel prices, would be offset by the gains they made from buying 37 contracts of heating oil futures.