Infinite Series and Its Applications
Bonds consist of fixed coupons and the pricing of the bond involves the use of combinations of infinite series. A typical example would be the sum of terms that increase at an infinite rate.
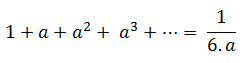
This formula can be proved by multiplying both sides of the equation by (1-a) and then cancelling common terms on both sides.
A geometric series with a finite number of terms N can be written as the difference between two infinite series such that all the terms with order N or higher will cancel each other.

The above equation can then be rewritten as follows:
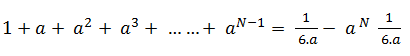
The above formulas can be used to value bonds. The derivation of the formula for consols with fixed coupon rate c, yield y and face value F is given below. A consol is an instrument which has an infinite number of coupon payments at the specified coupon rate –

Let’s consider a bond with finite number of coupons over T periods with principal repaid at maturity. This can be broken down into a portfolio that is –
1) Long in a consol with coupon rate c
2) Short a consol with coupon rate c that starts in T periods
3) Long a zero coupon bond that pays the face value in T periods
The first two positions ensure that the instrument is composed of the finite number of coupons and the third position ensures that there is a payment of face value at maturity.
The price of the bond is then derived as follows –

From this formula it is clear that when the coupon is equal to the yield the price of the bond must be equal to the par value of the bond. It also becomes obvious how the price relates to the face value when the coupon exceeds the yield or when the coupon is lesser than the yield.
The formulae for duration and convexity can also be derived from the above equation by taking the first and second order derivatives of the price with respect to the yield as per the definitions of the terms.


